Differentials Rules . given a function \(y = f\left( x \right)\) we call \(dy\) and \(dx\) differentials and the relationship between them is given. For instance, given the function w = g(x,y,z) w =. Both derivatives and differentials (and, in fact, all forms of differentiation that you may learn. In this section (and in some sections to follow) we. we find our next differentiation rules by looking at derivatives of sums, differences, and constant multiples of functions. 7.1 review of single variable differentiation. so if y = 6x2 + 11x − 13, we can immediately compute y′ = 12x + 11. there is a natural extension to functions of three or more variables. in other words, to differentiate a sum or difference all we need to do is differentiate the individual terms and then.
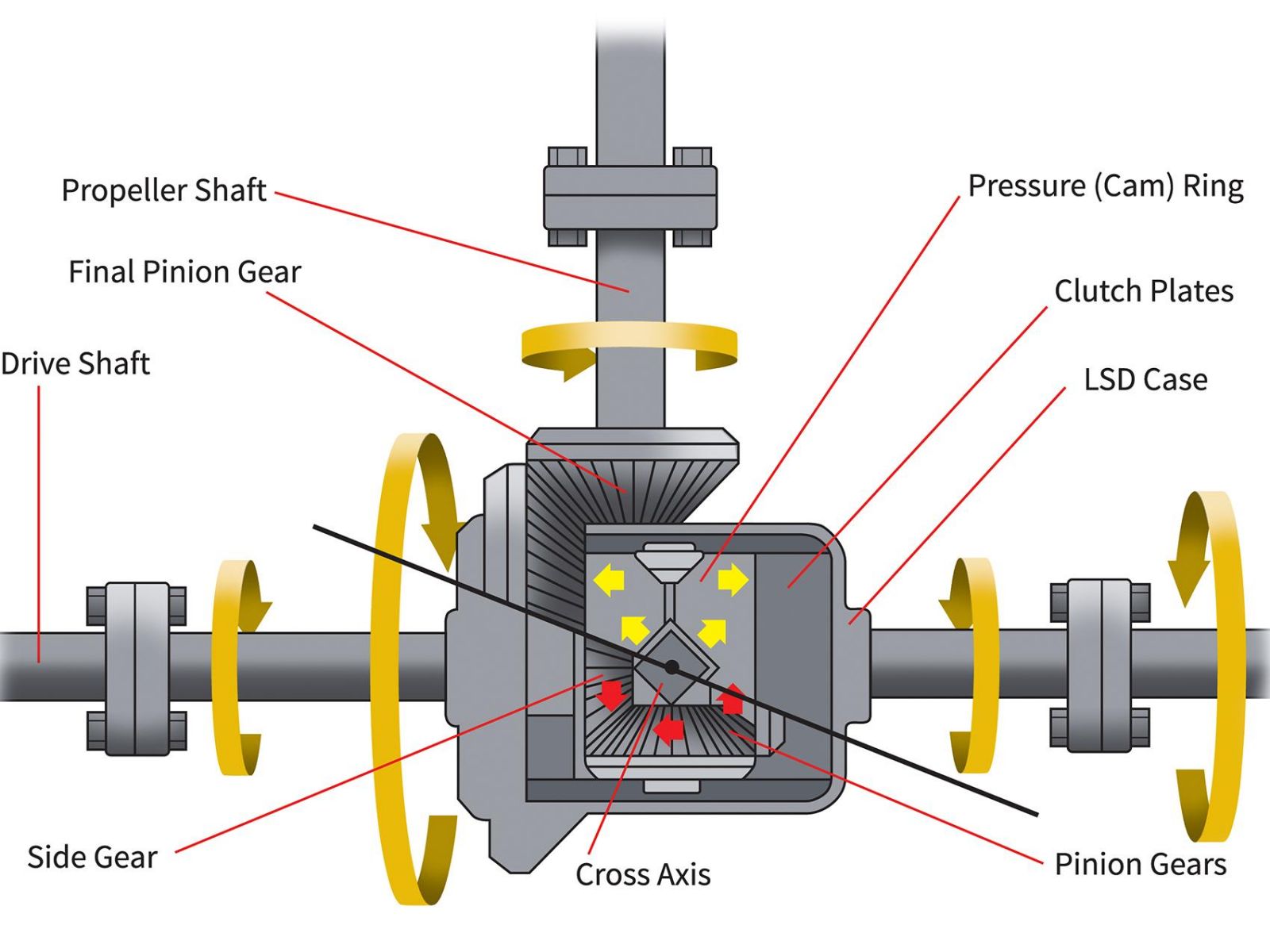
from www.carexpert.com.au
Both derivatives and differentials (and, in fact, all forms of differentiation that you may learn. there is a natural extension to functions of three or more variables. so if y = 6x2 + 11x − 13, we can immediately compute y′ = 12x + 11. 7.1 review of single variable differentiation. In this section (and in some sections to follow) we. in other words, to differentiate a sum or difference all we need to do is differentiate the individual terms and then. we find our next differentiation rules by looking at derivatives of sums, differences, and constant multiples of functions. For instance, given the function w = g(x,y,z) w =. given a function \(y = f\left( x \right)\) we call \(dy\) and \(dx\) differentials and the relationship between them is given.
Differentials explained CarExpert
Differentials Rules For instance, given the function w = g(x,y,z) w =. we find our next differentiation rules by looking at derivatives of sums, differences, and constant multiples of functions. In this section (and in some sections to follow) we. there is a natural extension to functions of three or more variables. given a function \(y = f\left( x \right)\) we call \(dy\) and \(dx\) differentials and the relationship between them is given. in other words, to differentiate a sum or difference all we need to do is differentiate the individual terms and then. so if y = 6x2 + 11x − 13, we can immediately compute y′ = 12x + 11. 7.1 review of single variable differentiation. Both derivatives and differentials (and, in fact, all forms of differentiation that you may learn. For instance, given the function w = g(x,y,z) w =.
From www.slideserve.com
PPT Differential Calculus PowerPoint Presentation, free download ID Differentials Rules 7.1 review of single variable differentiation. we find our next differentiation rules by looking at derivatives of sums, differences, and constant multiples of functions. in other words, to differentiate a sum or difference all we need to do is differentiate the individual terms and then. so if y = 6x2 + 11x − 13, we can immediately. Differentials Rules.
From www.pinterest.jp
Differential Calculus The Rules of Differentiation Differential Differentials Rules Both derivatives and differentials (and, in fact, all forms of differentiation that you may learn. For instance, given the function w = g(x,y,z) w =. there is a natural extension to functions of three or more variables. In this section (and in some sections to follow) we. we find our next differentiation rules by looking at derivatives of. Differentials Rules.
From www.matheno.com
A.5 Differentials; Begin to Determine df/dx at x=a Differentials Rules given a function \(y = f\left( x \right)\) we call \(dy\) and \(dx\) differentials and the relationship between them is given. we find our next differentiation rules by looking at derivatives of sums, differences, and constant multiples of functions. For instance, given the function w = g(x,y,z) w =. In this section (and in some sections to follow). Differentials Rules.
From durofy.com
Differential Calculus The Basic Derivatives Durofy Business Differentials Rules In this section (and in some sections to follow) we. For instance, given the function w = g(x,y,z) w =. so if y = 6x2 + 11x − 13, we can immediately compute y′ = 12x + 11. Both derivatives and differentials (and, in fact, all forms of differentiation that you may learn. given a function \(y =. Differentials Rules.
From www.fity.club
Differentiation Rules Differentials Rules so if y = 6x2 + 11x − 13, we can immediately compute y′ = 12x + 11. in other words, to differentiate a sum or difference all we need to do is differentiate the individual terms and then. In this section (and in some sections to follow) we. we find our next differentiation rules by looking. Differentials Rules.
From www.studypool.com
SOLUTION Integration and differentiation formula sheet Studypool Differentials Rules 7.1 review of single variable differentiation. For instance, given the function w = g(x,y,z) w =. in other words, to differentiate a sum or difference all we need to do is differentiate the individual terms and then. Both derivatives and differentials (and, in fact, all forms of differentiation that you may learn. given a function \(y = f\left(. Differentials Rules.
From www.youtube.com
Total Differential YouTube Differentials Rules Both derivatives and differentials (and, in fact, all forms of differentiation that you may learn. there is a natural extension to functions of three or more variables. so if y = 6x2 + 11x − 13, we can immediately compute y′ = 12x + 11. 7.1 review of single variable differentiation. given a function \(y = f\left(. Differentials Rules.
From www.wikihow.com
4 Ways to Solve Differential Equations wikiHow Differentials Rules given a function \(y = f\left( x \right)\) we call \(dy\) and \(dx\) differentials and the relationship between them is given. so if y = 6x2 + 11x − 13, we can immediately compute y′ = 12x + 11. in other words, to differentiate a sum or difference all we need to do is differentiate the individual. Differentials Rules.
From 814aprilsingletonkabar.blogspot.com
Differentiation Rules Pdf Differentials Rules 7.1 review of single variable differentiation. Both derivatives and differentials (and, in fact, all forms of differentiation that you may learn. For instance, given the function w = g(x,y,z) w =. there is a natural extension to functions of three or more variables. In this section (and in some sections to follow) we. given a function \(y =. Differentials Rules.
From www.slideserve.com
PPT Chapter 3 Differentiation Rules PowerPoint Presentation, free Differentials Rules we find our next differentiation rules by looking at derivatives of sums, differences, and constant multiples of functions. given a function \(y = f\left( x \right)\) we call \(dy\) and \(dx\) differentials and the relationship between them is given. For instance, given the function w = g(x,y,z) w =. 7.1 review of single variable differentiation. so if. Differentials Rules.
From www.studocu.com
Calculus Cheat Sheet DIFFERENTIATION FORMULAS Limits & Derivatives Differentials Rules so if y = 6x2 + 11x − 13, we can immediately compute y′ = 12x + 11. in other words, to differentiate a sum or difference all we need to do is differentiate the individual terms and then. there is a natural extension to functions of three or more variables. 7.1 review of single variable differentiation.. Differentials Rules.
From www.tutopiya.com
Mastering Basic Differentiation Rules Cambridge IGCSE Mathematics Differentials Rules In this section (and in some sections to follow) we. in other words, to differentiate a sum or difference all we need to do is differentiate the individual terms and then. 7.1 review of single variable differentiation. Both derivatives and differentials (and, in fact, all forms of differentiation that you may learn. For instance, given the function w =. Differentials Rules.
From www.slideserve.com
PPT Exact differentials and the theory of differential equations Differentials Rules Both derivatives and differentials (and, in fact, all forms of differentiation that you may learn. we find our next differentiation rules by looking at derivatives of sums, differences, and constant multiples of functions. in other words, to differentiate a sum or difference all we need to do is differentiate the individual terms and then. so if y. Differentials Rules.
From www.slideserve.com
PPT Math 1304 Calculus I PowerPoint Presentation, free download ID Differentials Rules in other words, to differentiate a sum or difference all we need to do is differentiate the individual terms and then. 7.1 review of single variable differentiation. given a function \(y = f\left( x \right)\) we call \(dy\) and \(dx\) differentials and the relationship between them is given. For instance, given the function w = g(x,y,z) w =.. Differentials Rules.
From cebqlpkh.blob.core.windows.net
Different Rules at Justin Ramos blog Differentials Rules in other words, to differentiate a sum or difference all we need to do is differentiate the individual terms and then. so if y = 6x2 + 11x − 13, we can immediately compute y′ = 12x + 11. Both derivatives and differentials (and, in fact, all forms of differentiation that you may learn. In this section (and. Differentials Rules.
From reevesapcalcbc.weebly.com
Derivative Rules AP Calc BC Differentials Rules 7.1 review of single variable differentiation. given a function \(y = f\left( x \right)\) we call \(dy\) and \(dx\) differentials and the relationship between them is given. For instance, given the function w = g(x,y,z) w =. In this section (and in some sections to follow) we. in other words, to differentiate a sum or difference all we. Differentials Rules.
From www.slideserve.com
PPT Chapter 3 Differentiation Rules PowerPoint Presentation, free Differentials Rules For instance, given the function w = g(x,y,z) w =. Both derivatives and differentials (and, in fact, all forms of differentiation that you may learn. given a function \(y = f\left( x \right)\) we call \(dy\) and \(dx\) differentials and the relationship between them is given. there is a natural extension to functions of three or more variables.. Differentials Rules.
From www.tes.com
A level Maths DIFFERENTIATION Rules (Edexcel) Teaching Resources Differentials Rules we find our next differentiation rules by looking at derivatives of sums, differences, and constant multiples of functions. 7.1 review of single variable differentiation. For instance, given the function w = g(x,y,z) w =. in other words, to differentiate a sum or difference all we need to do is differentiate the individual terms and then. there is. Differentials Rules.